A body that can not be deformed is called rigid body. In fact rigid body is an ideal concept. No body is rigid; some bodies are also elastic and can be deformed. The interesting thing of elastic nature of bodies is that they come back to their original state after being deformed considering that the force applied is small enough.
Stress and Strain
Here we discuss the relationship between stress and strain. The idea of stress and strain comes from the force that causes deformation. The main idea of stress and strain is that the stress is defined in terms of the force per unit area and the strain in terms of the change in dimension per unit initial dimension. We discuss three types of stress and strain below.
Tensile Stress and Strain
In Figure 2 you can see a rod of cross-sectional area \(A\) and a force of magnitude \(F\) acts perpendicular to the cross-section on the right end of the rod. The initial length of the rod without any force is \(L_i\). The force on the rod stretches the rod and the final length is \(L_i + \Delta L\).

The tensile stress is ratio of the force on the rod perpendicular to the cross-sectional area to the cross-sectional area \(A\) that is,
\[\text{Tensile Stress}=\frac{{F}}{A}\]
The force on the rod changes the length of the rod to the final length \(L_i + \Delta L\), so the tensile strain is the ratio of the change in length \(\Delta L\) to the initial length \(L_i\). Therefore,
\[{\text{Tensile Strain}} = \frac{\Delta L}{L_i}\]
The ratio of the tensile stress to the tensile strain is constant if the force is small enough which is called Young's Modulus denoted by \(Y\).
\[Y = \frac{{{\text{Tensile Stress}}}}{{{\text{Tensile Strain}}}} = \frac{{FL}}{{A{\kern 1pt} \Delta L}} \tag{1} \label{1}\]
On the other hand we can also consider the compression of the rod instead of stretching it. If the rod is compressed, the stress is compressive stress and corresponding strain is compressive strain. Note that in Figure 2 the same magnitude of force should be applied on the left end to apply the force on the right end.
Shear Stress and Strain
In this case a force acts on a surface being parallel to the surface (not perpendicular). See in Figure 3 that a force of magnitude \(F\) is applied to the top surface of a box of area \(A\) in such a way that the surface and the force are both parallel. The same magnitude of force should be there at the bottom of the box parallel to the surface.
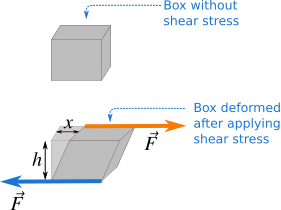
The shear stress is the ratio of the force parallel to the surface to the area of the surface which is,
\[\text{Shear Stress}=\frac{F}{A}\]
The parallel force on the surface changes the shape of the box. The ratio of \(x\) to the height \(h\) in Figure 3 is the shear strain. Thus,
\[{\text{Shear Strain}} = \frac{x}{h}\]
The ratio of the shear stress to the shear strain is constant for forces that are small enough called shear modulus denoted by \(S\) which is,
\[S = \frac{{{\text{Shear Stress}}}}{{{\text{Shear Strain}}}} = \frac{{Fx}}{{A{\kern 1pt} h}} \tag{2} \label{2} \]
Bulk Stress and Strain
A box is immersed in a fluid in Figure 4. Suppose the box experiences a uniform force at every point on the surface perpendicular to the surface. If the initial pressure before immersing the box is \({P_i} = \frac{{{F_i}}}{A}\) and the final pressure after immersing the box is \({P_f} = \frac{{{F_f}}}{A}\), then the change in pressure is \(\Delta P = \frac{{{F_f}}}{A} - \frac{{{F_i}}}{A} = \frac{{\Delta F}}{A}\). If the initial pressure on the box is \(P_i\), its final pressure after immersing in the fluid is \(P_i + \Delta P\) where \(\Delta P\) is the change in pressure. The resulting change in pressure decreases the volume of the box. Here the change in pressure \(\Delta P = \frac{{\Delta F}}{A}\) is the bulk stress.
\[{\text{Bulk Stress}} = \frac{{\Delta F}}{A} = \Delta P\]
Note that the pressure acts on the entire surface of the box perpendicular to the surface. The change in pressure causes the deformation of the box that is, the volume is decreased in Figure 4.
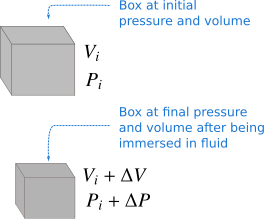
The initial volume of the box is \(V_i\) and the final volume is \(V_i + \Delta V\), so the change in volume is \(\Delta V\). Notice here that the volume has decreased due to the increase in pressure, hence \(\Delta V\) is negative and \(\Delta P\) is positive. Now the bulk strain is the ratio of the change in volume to the initial volume which is,
\[{\text{Bulk Strain}} = \frac{{\Delta V}}{{{V_i}}}\]
The final step is to know the bulk modulus, the ratio of the bulk stress to the bulk strain. The bulk modulus is constant for small deformations or forces. The limitation of small forces or deformations is to make the ratio of stress to strain constant. The bulk modulus denoted by \(B\) is
\[B = - \frac{{\Delta P\,{V_i}}}{{\Delta V}} \tag{3} \label{3}\]
The negative sign is put to make the bulk modulus a positive quantity because \(\Delta V\) and \(\Delta P\) always have opposite signs, that is if the pressure increases (\(\Delta P\) is positive), the volume decreases (\(\Delta V\) is negative). The reciprocal of the bulk modulus is called compressibility denoted by \(k\),
\[k = -\frac{{\Delta V}}{{\Delta P\,{V_i}}} \tag{4} \label{4}\]
Note that stress is not a vector quantity and its SI unit is \(N/{m^2}\). The Young's modulus, shear modulus and bulk modulus are called elastic moduli. The unit of elastic modulus is the same as the unit of stress because strain does not have any unit. The direct proportionality of stress and strain is another form of Hooke's law which is valid for small forces that do not exceed the proportionality limit and elastic modulus remains constant.
\[{\text{Elastic Modulus}} = \frac{{{\text{Stress}}}}{{{\text{Strain}}}}\]






