Let's derive the most useful equation known as Bernoulli's equation. First we consider a flow tube as shown in Figure 3 whose left end at height \(y_1\) has cross-sectional area \(A_1\) and right end at height \(y_2\) has cross-sectional area \(A_2\).
The fluid moves from the left end towards the right end. As in the continuity equation above we consider that the fluid is incompressible (that is the density is constant) with no viscosity and the flow is steady.
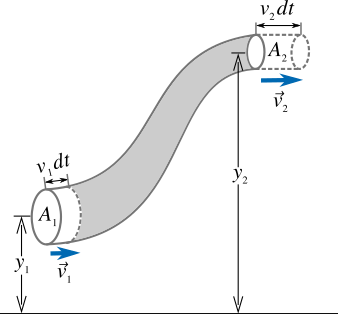
Let the speed of the flow on the left and right ends of the flow tube be \(v_1\) and \(v_2\) respectively. Let the pressure on the left end be \(P_1\) and that on the right end be \(p_2\).
The Bernoulli's equation connects pressure and flow speed at one cross-section at an elevation with pressure and flow speed at another cross-section at another elevation.
In a very small time interval \(dt\) the work done on the segment of the fluid due to the pressure \(P_1\) on the left end is \({W_1} = {P_1}{A_1}{v_1}dt\). The force due to the pressure \(P_2\) on the right end does negative work because it opposes the flow so the work done by this force is \({W_2} = -{P_2}{A_2}{v_2}dt\). So the net work done by the pressure of the surrounding fluid on the fluid segment is
\[dW = {W_1} - {W_2} = {P_1}{A_1}{v_1}dt - {P_2}{A_2}{v_2}dt \tag{2} \label{2}\]
The only conservative force acting on the segment of the fluid is gravity, so the work done given by Eq. \eqref{2} is equal to the change in total mechanical energy of the system.
Since the fluid is incompressible without viscosity and the flow is steady, the mass of the fluid which enters the left end in the time interval \(dt\) is the same as the mass of the fluid which leaves the right end in the same time.
And therefore, \(dm = \rho {A_1}{v_1}dt = \rho {A_2}{v_2}dt\) which implies our continuity equation \({A_1}{v_1} = {A_2}{v_2}\). In other words the volume of the fluid which enters the left end in the time interval \(dt\) is the same as the volume of the fluid which leaves the right end in the same time interval and you can write \(dV = {A_1}{v_1}dt = {A_2}{v_2}dt\) and again \({A_1}{v_1} = {A_2}{v_2}\). The Eq. \eqref{2} can be rewritten as,
\[dW = ({P_1} - {P_2})dV \tag{3} \label{3}\]
The kinetic and potential energies of the shaded portion of the fluid in Figure 3 remain the same for steady flow. So the change in kinetic energy is only due to the change in speed of the fluid element of mass \(dm\). Therefore, the change in kinetic energy \(dK\) of the fluid between the two ends is
\[dK = \frac{1}{2}dm{\kern 1pt} {\kern 1pt} v_2^2 - \frac{1}{2}dm\,v_1^2 = \frac{1}{2}\rho dV(v_2^2 - v_2^2) \tag{4} \label{4}\]
In the time interval \(dt\) the change in potential energy of the fluid segment means the fluid element of volume \(dV\) rises a height of \(y_2-y_1\) and therefore, the change in potential energy \(dU\) is
\[dU = dm{\kern 1pt} g({y_2} - {y_1}) = \rho dVg({y_2} - {y_1}) \tag{5} \label{5}\]
And the total change in mechanical energy is \(dE = dK + dU\) which is equal to the work \(dW\) done by the pressures of the surrounding fluid in Eq. \eqref{3}. Hence,
\[\begin{align*} ({P_1} - {P_2})dV &= \frac{1}{2}\rho dV(v_2^2 - v_1^2) + \rho dV{\kern 1pt} g({y_2} - {y_1})\\ {\rm{or,}}\quad ({P_1} - {P_2}) &= \frac{1}{2}\rho (v_2^2 - v_1^2) + \rho {\kern 1pt} g({y_2} - {y_1}) \tag{6} \label{6} \end{align*}\]
The Eq. \eqref{6} is called Bernoulli's equation. Rearranging the equation you'll find,
\[\begin{align*} {P_1} + \frac{1}{2}\rho v_1^2 + \rho g{y_1} &= {P_2} + \frac{1}{2}\rho v_2^2 + \rho g{y_2}\\ \tag{7} \label{7} {\rm{or,}}\quad P + \frac{1}{2}\rho v_{}^2 + \rho gy &= {\rm{constant}} \end{align*}\]
The Eq. \eqref{7} shows that the quantity \(P + \frac{1}{2}\rho v_{}^2 + \rho gy\) remains constant throughout the flow tube. Note that Bernoulli's equation is valid for an incompressible fluid with zero viscosity and flow should be steady.






