Wave is a disturbance which travels. For example, if you through a stone in a pond you see the ripple due to the disturbance created by the stone; the ripple is the disturbance created by the stone which traveled in the form of wave (Figure 1). Particularly travelling disturbance is called wave. Also the sound waves you here are created by the disturbance in the air.
Waves which need a medium to travel are called mechanical waves while the electromagnetic waves do not need any medium to travel. Sound waves always need a medium to travel, so they are mechanical waves. When a wave travels in a medium the particles in the medium move. For example, you are stretching a rope under tension whose right end is attached to a rigid support as in Standing Waves and Normal Modes
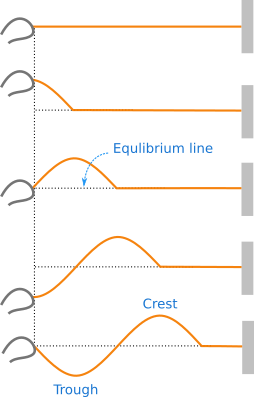
The real wave produced by your hand is not as smooth as shown in Figure 2 but you got the wave idea which your hand can produce! As the wave travels the particles of the string are displaced. The particles move in the direction perpendicular to the direction of the propagation of the wave. And we consider that the wave travels in positive x-direction of our coordinate system. A mechanical wave in which the particles of the medium move in the direction perpendicular to the direction of the propagation of the wave is called transverse wave. Figure 2 shows an example of transverse wave.

In Figure 3, a gas is inside a container with movable frictionless piston. As the piston is moved forward and backward a disturbance is created in the gas which then travels in the form of wave. We consider that the wave travels in positive x-direction of our coordinate system. Successive back and forth motions of the piston create successive wave pulses. The particles move as they experience the disturbance created by the movable piston and they also show the back and forth motion. It means the particles move back and forth as the wave (disturbance) travels. A mechanical wave in which the particles in its medium move in the direction parallel or anti-parallel to the direction of wave propagation is called longitudinal wave. Therefore, the wave in Figure 3 is a longitudinal wave.
Mechanical Simple Harmonic Waves
Now we consider a special situation of transverse and longitudinal waves. If the left end of the string in Figure 2 is moved up and down in simple harmonic motion about the equilibrium position, every particle in the medium move in simple harmonic motion as the disturbance or wave travels and we gettransverse simple harmonic wave. Similarly, if the piston in Figure 3 is moved back and forth in simple harmonic motion, every particle in the container move in simple harmonic motion as the disturbance reaches the particle and you'll get longitudinal simple harmonic wave.
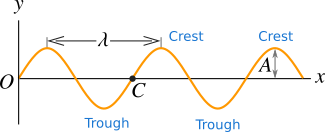
If we plot a graph of transverse or longitudinal simple harmonic wave of the displacement of particle \(y\) in the medium with position \(x\), we get a curve like shown in Figure 4. The graph is obtained at a particular instant of time \(t\). All particles in the medium move in simple harmonic motion and in a time period of one complete oscillation of a particle the wave travels a distance called wavelength denoted by lambda \(\lambda\). In Figure 4 the wave travels a distance equal to \(OC\) in a time period that is, \(\lambda = OC\). The distance \(\lambda\) is also equal to the distance between successive crests or troughs or it is equal to the distance between successive particles moving in phase. The absolute value of maximum displacement of a particle from equilibrium position is amplitude denoted by \(A\).
The amplitude and time period of a simple harmonic wave are constant until you change but the wave produced by your hand as in Figure 2 can not have constant amplitude and time period. The human hand is not precise to produce a simple harmonic wave. The wave travels a distance equal to it's wavelength \(\lambda\) in a time period \(T\) and if \(v\) is the speed of the wave, it is given by the expression,
\[v=\frac{\lambda }{T}=\lambda f \tag{1} \label{1}\]
where \(f\) is the frequency of the wave which is \(f = 1/T\). The speed of mechanical waves is determined by the mechanical properties of the medium not by its frequency or wavelength. Large number of waves with different frequencies can move with the same wave speed whose wavelengths are different to make the wave speed constant; it means as frequency increases, wavelength decreases and the wave speed is constant.






