When two mechanical waves of the same type from different sources overlap in a region of space, the displacement of any particle at a point in the medium which experiences the disturbance of the waves is the vector sum of the displacements due to individual waves in the same time. The vector sum of the displacements of a particle at a point due to all waves that reach the particle at that point in the same time is called superposition.
Suppose two waves reach a particle in a medium in the same time and \(y_1\) is the displacement of the particle due to one wave and \(y_2\) is the displacement due to another wave, you can find the resultant displacement \(y\) of the particle by the vector sum of individual displacements that is, \(\vec y = \vec y_1+ \vec y_2\).
On the other hand interference is the special case of superposition. Superposition of two or more waves of the same amplitude and frequency is what we call as interference. For superposition the waves can have any frequency and amplitude but it's not true for the interference of waves.
What's the definition of standing wave and normal modes?
When a wave is reflected from a boundary, the reflected wave overlaps the incident wave. We consider a sinusoidal transverse wave along a string traveling in positive x-direction as in Figure 1. When the wave is reflected at the fixed end, it overlaps the incident wave and the interference of the incident and reflected waves turns into another wave called standing wave.

In Figure 1 the reflected wave is travelling in negative x-direction. When the incident and reflected waves overlap some points are developed in the medium. The points where a particle in the medium do not move at all and the displacement amplitude is zero are called nodes denoted by \(N\). Other type of points where there is a maximum displacement of a particle are called antinodes denoted by \(A\). The nodes and antinodes are shown in Figure 1. In standing wave the net transfer of energy in a particular direction is zero that is the same amount of energy which flows towards the right (towards +x-direction) also flows towards the left (towards -x-direction) and net transfer is zero. Therefore, energy is not transferred in a standing wave.
We know that the wave function of a simple harmonic wave travelling in positive x-direction is \(y_1 = A \cos (kx- \omega t)\) and the wave function for negative x-direction is \(y_2 = A \cos (kx + \omega t)\). The resultant wave function of these two waves is \(y = y_1 + y_2\). The wave reflected at the fixed end is inverted so we write \(y_2 = - A \cos (kx - \omega t)\). You may know the trigonometric identities of cosine function such as \(\cos (A + B) = \cos A\cos B - \sin A\sin B\) and \(\cos (A - B) = \cos A\cos B + \sin A\sin B\). Now you can find the resultant wave function which is
\[y = y_1 + (-y_2)=(2A\sin kx)\sin \omega t \tag{1} \label{1}\]
The above equation shows the wave function for the standing wave. At nodes the displacement of a particle from equilibrium position (displacement amplitude) is zero and hence \(\sin kx = 0\). Therefore, at nodes \(kx = 0, \pi, 2\pi, 3\pi\) and so on which implies \(x = 0, \lambda /2, 2\lambda/2, 3\lambda/2\) and so on. Later you'll see some special modes of frequencies called normal modes of a standing wave.
What are normal modes?
Normal mode of an oscillating system means that all particles in a medium oscillate in simple harmonic motion with the same frequency. Here we consider that a string of length \(L\) is stretched and both of its ends are fixed as shown in Figure 2. A disturbance is created and a simple harmonic wave travels along the length of the string. Both ends fixed means the both ends are the nodes which do not move. Note that the distance between two successive nodes is \(\lambda /2\). The first standing wave has two nodes and one antinode (see Figure 2).
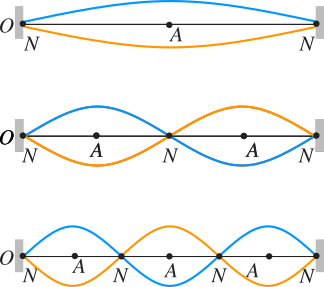
And therefore for the first standing wave, the length \(L\) is equal to \(\lambda / 2\) that is, \(L = \lambda/ 2\) or \(\lambda = 2L\). So we can find the first frequency of the standing wave by using the relationship \(v=\lambda f\):
\[f_1 = \frac{v}{{2L}} \tag{2} \label{2}\]
The above equation shows the first possible frequency with two nodes (and one antinode) called fundamental frequency and the corresponding normal mode is the first normal mode. Another standing wave can be formed with three nodes and two antinodes and you can write \(L = 2\lambda/2\) or \(\lambda = L\). So the frequency of the standing wave with three nodes and two antinodes is
\[f_2 = \frac{v}{L} = \frac{{2v}}{{2L}} \tag{3} \label{3}\]
Similarly other standing wave is obtained with four nodes and three antinodes. Hence, the length is \(L = 3\lambda /2\) or \(3\lambda = 2L\) and the corresponding frequency is
\[{f_3} = \frac{{3v}}{{2L}} \tag{4} \label{4}\]
and so on. You can find using Eqs. \eqref{2}, \eqref{3} and \eqref{4}, that the frequency of any normal mode of the standing wave along the string fixed at both ends is \(f_n = nf_1\) where \(n = 1, 2, 3, 4, 5\) etc. You saw that the normal mode frequency \(f_n\) of the standing wave along the string is \(f_n = nf_1\) and hence there are infinite number of normal modes possible on the string. The frequencies of various normal modes given by \(f_n = nf_1\) is called harmonic series and a particular frequency in the harmonic series is called harmonic.
What are normal modes in standing sound wave?
Sound waves are pressure fluctations as it travels in the form of compressions and rarefactions. Unlike the transverse standing waves along the stretched string discussed earlier, there are two kinds of nodes and antinodes in sound waves. A displacement node is a point in sound wave where the displacement of a particle is always zero but at the displacement node the pressure variation is maximum so the displacement node is also called pressure antinode (pressure variation is maximum). In the similar way, a displacement antinode is a point where the displacement of a prticle is maximum but at the displacement antinode the pressure variation is zero so the displacement antinode is also called pressure node (the pressure does not change). Here we discuss a simple harmonic standing sound wave whose wave function is the same as given by Eq. \eqref{1}. Here two simple harmonic sound waves overlap after reflection and standing wave is formed. We consider a system of air inside a pipe (air column) or an organ pipe. Organ pipe is a pipe to produce sound.
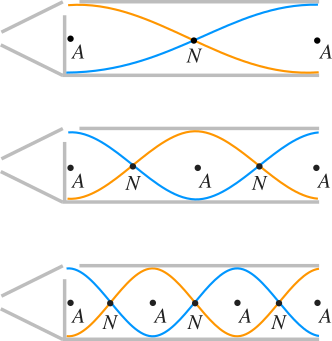
An organ pipe can be open or closed. In Figure 3 you can see an organ pipe of length \(L\) open at both ends. Note that the left end of the pipe is also open end (which is not completely closed). When the air is blown into the pipe, vibrations are created and those vibrations create disturbance which then travels in the form of sound towards the right open end. The open ends of the pipe are open to the atmosphere and the air in the atmosphere creates boundary conditions and the wave is reflected at the open end. Both ends are open so there should be displacement antinodes or pressure nodes at the ends of the pipe. The first standing wave is created when there are two displacement antinodes at the ends and one displacement node between the displacement antinodes. The distance between one displacement node to its nearby displacement antinode is always \(\lambda /4\) and therefore you can write \(L = 2\lambda/ 4 =\lambda /2\) or \(\lambda = 2L\) for the first standing wave. So the first normal mode frequency \(f_1\) is
\[{f_1} = \frac{v}{{2L}} \tag{5} \label{5}\]
The second standing wave will have three antinodes and two nodes (Figure 3) and therefore \(L = 4\lambda/4 = \lambda\). So, you can find the second normal mode frequency \(f_2\) as
\[{f_2} = \frac{v}{L} = \frac{{2v}}{{2L}} \tag{6} \label{6}\]
Similarly you can find the third normal mode frequency of third standing standing wave and in that case the standing wave will have four antinodes and three nodes (Figure 3). So, \(L = 6\lambda/4\) or \(L = 3\lambda/2\) and
\[{f_3} = \frac{{3v}}{{2L}} \tag{7} \label{7}\]
You can similarly find other normal mode frequencies and you'll find that any normal mode frequency \(f_n\) is given by the relationship \(f_n = nf_1\) where \(n = 1, 2, 3, 4...\) etc. The series of frequencies given by \(f_n = nf_1\) are called harmonics so the first harmonic occurs when \(n =1 \) and the second harmonic occurs when \(n = 2\) and so on.
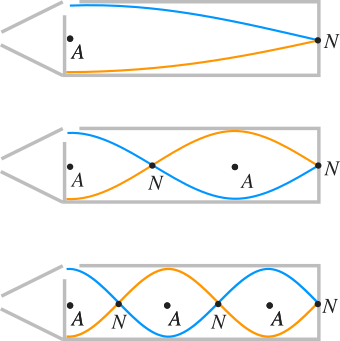
Another case of the same organ pipe as before is shown in Figure 4 but in this case the right end of the pipe is closed. Such an organ pipe is called closed organ pipe. Note that the left end is still open; it is not possible to make a sound in an organ pipe whose both ends are closed. The right end is closed so the particles at that end should not move; it means the right end is always the displacement node or pressure antinode while the left end is always displacement antinode or pressure node. The first standing wave is set up with the first normal mode frequency when there is only one displacement antinode at the left end and only one displacement node at the right end (Figure 4) so \(L = \lambda/4\) and therefore the first normal mode frequency for the closed pipe is
\[{f_1} = \frac{v}{{4L}} \tag{8} \label{8}\]
And the second normal mode frequency is obtained when there are two displacement antinodes and two displacement nodes (Figure 4). So, \(L = 3\lambda/4\) and \(f_2\) is
\[{f_2} = \frac{{3v}}{{4L}} \tag{9} \label{9}\]
Similarly, you can also find the third normal mode frequency and in that case you can again investigate in Figure 4 and find that there are three antinodes and three nodes. So, \(L = 5\lambda/4\) and \(f_3\) is
\[{f_3} = \frac{{5v}}{{4L}} \tag{10} \label{10}\]
In the similar way any normal mode frequency \(f_n\) for the closed organ pipe is given by \(f_n = (2n-1)f_1\) where \(n = 1, 2, 3, 4, ...\) . Note here that the even harmonics are missing for closed organ pipe.






