The heat and temperature are entirely different things but we can define the hotness or coldness of a body or material in terms of it's temperature. This is very familiar to you that when a body is heated (supplied heat to it), it's temperature and volume increase. So the temperature of a material can be measured in terms of the expansion of a particular material arranged in a way which can be calibrated on a scale. One example is the liquid thermometer.

In liquid thermometer, usually mercury or alcohol are taken inside a tube. When the tube with liquid is placed in thermal contact with a hot body, the liquid level rises in the tube (see Figure 1). The tube is calibrated and you can measure the temperature of the body.
Celsius and Fahrenheit temperature scales
The most commonly used temperature scales are Celsius and Fahrenheit temperature scales. We ponder an example of a thermometer shown in Figure 1.
In Celsius scale the zero of the thermometer is calibrated at the point where the liquid in the thermometer is in thermal equilibrium with the constant temperature of the mixture of ice and water (freezing point).
Similarly, the 100 of the thermometer is the point where the liquid rises in the capillary tube and comes in thermal equilibrium with the temperature of the mixture of water and steam (boiling point).
The length between these two points is divided into 100 equal parts and the smallest part is called one degree Celsius written as \(1{{\kern 1pt} ^ \circ }{\rm{C}}\). There are 100 degrees between freezing and boiling temperatures of water in Celsius scale.
In Fahrenheit scale the temperature of the freezing point of water is \(32{{\kern 1pt} ^ \circ }{\rm{F}}\) (thirty-two degrees Fahrenheit) and the temperature of the boiling point is \(212{{\kern 1pt} ^ \circ }{\rm{F}}\). Note that in Fahrenheit scale, the smallest value is called one degree Fahrenheit written as \(1{{\kern 1pt} ^ \circ }{\rm{F}}\).
There are 180 degrees between freezing and boiling temperatures of water in Fahrenheit scale, so you can convert the temperature in Celsius scale into Fahrenheit scale by using the expression below:
\[{T_F} = 32{}^ \circ {\rm{F}} + \frac{9}{5}{T_C} \tag{1} \label{1}\]
where \(T_F\) and \(T_C\) represent the temperatures in Fahrenheit and Celsius scales respectively. You can also convert the temperature in Fahrenheit scale in Celsius scale by solving for \(T_C\) in the above equation:
\[{T_C} = ({T_F} - 32{}^ \circ {\rm{F)}}\frac{5}{9} \tag{2} \label{2}\]
There are different kinds of thermometers which depend on the material used. Material dependent thermometers always have discrepancies. For example, mercury and alcohol have different expansion properties.
Therefore, mercury and alcohol thermometers can give the same temperature at the calibration points but give slightly different temperatures at intermediate points. The variations again increase when you measure the temperature beyond the calibration points.
All gases behave in the same way and for more precise measurement we need such a scale which is material independent and this can be achieved by a constant volume gas thermometer discussed below.
What is kelvin scale (constant volume gas thermometer)?
The constant volume gas thermometer is based on the relationship between pressure and temperature at constant volume; as the temperature increases, the pressure of the gas increases.
The constant volume gas thermometer is calibrated by finding the pressure of the gas at the temperature of freezing point of water (mixture of ice and water or ice point) and the pressure at the temperature of boiling point of water (mixture of water and steam or steam point).
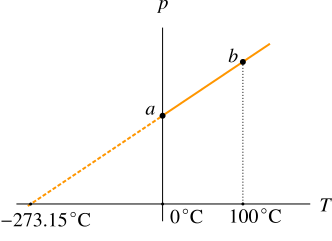
In Figure 2, the pressures of gas at \(0{{\kern 1pt} ^ \circ }{\rm{C}}\) and \(100{{\kern 1pt} ^ \circ }{\rm{C}}\) are measured. The point \(a\) where pressure is measured at \(0{{\kern 1pt} ^ \circ }{\rm{C}}\) is joined with with the point \(b\) where pressure is measured at \(100{{\kern 1pt} ^ \circ }{\rm{C}}\).
The straight line \(ab\) is produced backwards as shown by the dashed line in Figure 3 which meets the temperature axis at the temperature of \(-273.15{{\kern 1pt} ^ \circ }{\rm{C}}\). At this temperature the pressure of the gas is zero as shown by the graph and the temperature is called absolute zero. The zero pressure is not practically observed. The gases turn into liquids or solids in lower temperatures and the direct relationship between pressure and temperature is no longer valid.
The new temperature scale obtained by the graph in Figure 3 with its zero at \(-273.15{{\kern 1pt} ^ \circ }{\rm{C}}\) is called Kelvin scale of temperature; it means the zero Kelvin written as 0K not \(0{{\kern 1pt} ^ \circ }{\rm{K}}\) is equal to \(-273.15{{\kern 1pt} ^ \circ }{\rm{C}}\) and 273.15K is equal to \(0{{\kern 1pt} ^ \circ }{\rm{C}}\). Remember that \(\circ\) is not used in Kelvin scale. You can convert any temperature in Celsius scale into Kelvin scale by
\[{T_K} = 273.15 + {T_C} \tag{3} \label{3}\]
where \(T_K\) is the temperature in Kelvin scale. The SI unit of temperature is the Kelvin temperature from Kelvin scale.
The material dependent temperature scales can only measure the limited range of temperatures such as the mercury thermometer can not measure the temperature below freezing point of mercury. And material dependent thermometers are based on a particular planet or a particular material. The Kelvin scale of temperature can measure all possible temperatures in the universe and is the universal temperature scale.






