Kinetic Theory of an Ideal Gas

Gas molecules move randomly in any direction inside a container. Here we talk about the kinetic theory of an ideal gas. First we make assumptions considering ideal gas to derive our kinetic theory and find the relationship between temperature and kinetic energy of the ideal gas molecules.

Kinetic Theory of an Ideal Gas

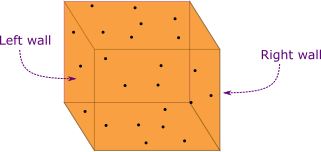
To understand the kinetic theory of an ideal gas we find the pressure the ideal gas exerts on the walls of a container. First consider an ideal gas inside a container like a box shown in Figure 1.

An ideal gas molecules do not occupy any volume of a container (in this case we say the gas molecules are point particles) and there is no intermolecular interaction between the molecules. We make the same assumptions we made in ideal gas to derive the kinetic theory.

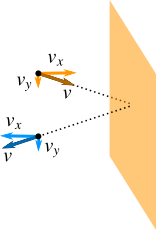
We also assume that the collisions of ideal gas molecules on the walls are perfectly elastic and therefore the momentum and kinetic energy both are conserved before and after the collisions.

In Figure 2 a molecule of mass $m$ collides on the right wall of the container. The y-component of velocity of the molecule remains unchanged before and after the collision, so the change in y-component of momentum is zero. Only the x-component of velocity changes.

The x-component of momentum before collision is $mv_{x}$ and after collision is $-mv_{x}$. Therefore, the magnitude of the change in momentum of the molecule is $2mv_{x}$.

In time $dt$ the molecules having the possibility to collide on the right wall of area $A$ are within a distance $v_{x} dt$ from the wall, so the volume containing molecules having the possibility to collide on the wall in time $dt$ is $Av_{x} dt$.

If $N$ is the total number of molecules and $V$ is the volume of the container, the number density is $N/V$. Then, the total number of molecules which has the possibility to collide on the wall is the product of volume $Av_{x} dt$ and the number density which is $\frac{N}{V}(A{v_{x}}dt)$.

The average number of molecules that collide on the wall is the half of this, that is $\frac{N}{2V}(A{v_{x}}dt)$. So, the total change in x-component of momentum $dP_x$ of the colliding molecules in time $dt$ is

\[d{P_x} = \frac{N}{{2V}}(A{v_{x}}dt)(2m{v_{x}}) = \frac{N}{V}Amv_{x}^2dt \tag{1} \label{1}\]

Its wrong to assume the same magnitude of velocity for all particles so we replace $v_x^2$ in above equation by the average value of $v_x^2$ which is ${\left( {v_x^2} \right)_{av}}$. The force $F$ the molecules exert on the right wall is the rate of change of momentum:

\[F = \frac{{d{P_x}}}{{dt}} = \frac{N}{V}Am{\left( {v_x^2} \right)_{av}} \tag{2} \label{2}\]

And the pressure $p$ the molecules exert on the right wall is the force per unit area of the wall, that is $F$ divided by the area $A$:

\[\begin{align*} p &= \frac{N}{V}m{\left( {v_x^2} \right)_{av}} \tag{3} \label{3}\\ \Rightarrow pV &= Nm{\left( {v_x^2} \right)_{av}} \tag{4} \label{4} \end{align*}\]

The above equation Eq. \eqref{4} can be expressed in terms of the average of the square of velocity of all the molecules ${\left( {{v^2}} \right)_{av}}$.

The molecules move in any direction in random motion and also considering the motion of molecules in y and z directions we know ${\left( {v_{}^2} \right)_{av}} = {\left( {v_x^2} \right)_{av}} + {\left( {v_y^2} \right)_{av}} + {\left( {v_z^2} \right)_{av}}$.

For large number of molecules in random motion, the average of the square of the x-component of velocity of all molecules ultimately turns out to be the same as the average of the square of y-component of velocity and average of the square of z-component of velocity. So, ${\left( {v_x^2} \right)_{av}} = {\left( {v_z^2} \right)_{ay}} = {\left( {v_z^2} \right)_{av}}$ and you can find ${({v^2})_{av}} = 3{(v_x^2)_{av}}$. Now we can write Eq. \eqref{4} by replacing ${(v_x^2)_{av}}$ by $\frac{1}{3}{({v^2})_{av}}$ as

\[pV = \frac{1}{3}Nm{({v^2})_{av}} \tag{5} \label{5}\]

Multiplying the right hand side of the above equation by $1$ in the form of $2/2$ we can get:

\[pV = \frac{2}{3}N\left( {\frac{1}{2}m{{({v^2})}_{av}}} \right) \tag{6} \label{6}\]

The quantity inside parenthesis in the above equation is the average translational kinetic energy of a molecule. And the product of the number of all molecules and the average translational kinetic energy of a molecule is the total translational kinetic energy of all molecules. If we denote the total translational kinetic energy of all molecules by $K_\text{t}$ where the subscript $t$ represents translational, we can rewrite Eq. \eqref{6} as

\[pV = \frac{2}{3}{K_t} \tag{7} \label{7}\]

We obtained the Eq. \eqref{7} for an ideal gas, and therefore we can compare this equation with the ideal gas equation $pV = nRT$ to get the total translational kinetic energy of all the molecules in terms of absolute temperature:

\[\begin{align*} nRT &= \frac{2}{3}{K_t}\\ {\rm{and,}}\quad {K_t} &= \frac{3}{2}nRT \tag{8} \label{8} \end{align*}\]

Ultimately we obtained the idea of kinetic theory of an ideal gas, that is the Eq. \eqref{8} shows that the total kinetic energy of all molecules of an ideal gas is directly proportional to temperature.

You can also compare Eq. \eqref{7} with another form of ideal gas equation $pV = NkT$ (in terms of Boltzmann's constant $k$) and you'll get:

\[\begin{align*} \frac{2}{3}{{K}_{t}}&=NkT \\ \text{or,}\quad \frac{2}{3}N\left( \frac{1}{2}m{{({{v}^{2}})}_{av}} \right)&=NkT \\ \text{or,}\quad \frac{1}{2}m{{({{v}^{2}})}_{av}}&=\frac{3}{2}kT \tag{9} \label{9} \end{align*}\]

If the average translational kinetic energy of a single molecule is $k_t$ (in this case lower-case $k$; remember that $k_t$ and $k$ are different things), we have Eq. \eqref{9} in the form below:

\[{k_t} = \frac{3}{2}kT \tag{10} \label{10}\]

You can also find the value of ${{({{v}^{2}})}_{av}}$ using either Eq. \eqref{8} or Eq. \eqref{9}. Firstly we know ${{K}_{t}}=N\left( \frac{1}{2}m{{({{v}^{2}})}_{av}} \right)$ and using Eq. \eqref{8} and:

\[\begin{align*} N\left( \frac{1}{2}m{{({{v}^{2}})}_{av}} \right)&=\frac{3}{2}nRT \\ \text{or,}\quad {{({{v}^{2}})}_{av}}&=\frac{3nRT}{Nm} \tag{11} \label{11} \end{align*}\]

Number of moles $n$ is equal to the total number of molecules $N$ divided by the Avogrado's number $N_A$, that is $n=N/N_A$. Also the mass of a molecule $m$ multiplied by the Avagrado's number is called molar mass $M$. So, $M = N_A m$. Now we can replace $n$ in Eq. \eqref{11} by $N/N_A$ and solving gives:

\[{{({{v}^{2}})}_{av}}=\frac{3RT}{M} \tag{12} \label{12}\]

Secondly, you can also find the value of ${{({{v}^{2}})}_{av}}$ directly from Eq. \eqref{9} which is

\[{{({{v}^{2}})}_{av}}=\frac{3kT}{m} \tag{13} \label{13}\]

We introduce a new speed called rms speed (root-mean-square-speed) which is the square root of the average of the square of the velocity of molecules. So using the expressions of the average of the square of the velocity of molecules from Eqs. \eqref{12} and \eqref{13}, the rms speed of the molecules is

\[{{v}_{\text{rms}}}=\sqrt{{{({{v}^{2}})}_{av}}}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3RT}{M}} \tag{14} \label{14} \]

Mean Free Path

If you think ideal gas, you also think that the molecules do no occupy any volume of the container and therefore no collision between molecules is possible. Now we consider finite size of molecules (for real gases) so that we can talk about the collisions between molecules.

The average path (distance) travelled by a molecule between collisions is called mean free path. Consider that one molecule of a radius moves with all other molecules being at rest. When the molecule collies with another molecule, the distance between their centres is $r_1 + r_2$ where $r_1$ and $r_2$ are the radii of the colliding molecules.

If you consider all molecules are identical having the same radius $r$, the distance between the centres of the colliding molecules is $2r$. Here we suppose that all molecules have the same radius $r$. The moving molecule collides with another molecule whose centre lies within the distance $d = 2r$ as the molecule moves. In time $dt$ the molecule moves with speed $v$ and travels a distance of $vdt$, and it collides with the molecules whose centres lie in the cylindrical volume of $\pi d^2 vdt$ where $d = 2r$.

We know that the number density is the number of molecules per unit volume, that is $N/V$ where $N$ is the total number of molecules and $V$ is the total volume of the container. So, the number of molecules in the cylindrical volume is $\pi d^2 vdt (N/V)$. Now the mean free path is the distance traveled divided by the number of collisions. Note that the number of collisions is the same as the number of molecules (except the moving molecule) inside the cylindrical area we considered. Therefore, the mean free path is

\[\lambda =\frac{vdtV}{\pi {{d}^{2}}vdtN}=\frac{V}{\pi {{d}^{2}}N} \tag{15} \label{15}\]

In real situation all molecules move randomly not only one molecule and therefore the correct expression of the above equation is

\[\lambda = \frac{V}{{\sqrt {2{\kern 1pt} } \pi {d^2}N}} \tag{16} \label{16}\]

You can find the mean free time if you divide $\lambda$ by $v$.