The dynamics of thermal energy (or heat energy) is called thermodynamics. In thermodynamics we reveal the idea of converting heat energy into mechanical energy. And we do this on the basis of laws of thermodynamics. The usefulness of thermodynamics is that we don't need to consider the microscopic properties of a thermodynamic system and still can understand the thermodynamic process considering macroscopic properties by studying the relationship between state variables.
The change in any of the state variables causes a process. For example, heat flow can be considered as a process which is associated with the increase and decrease in temperature. Before discussing the first law of thermodynamics we should have the idea of thermodynamic system and internal energy of the system.
What is the relationship between thermodynamic system and internal energy?
A thermodynamic system is a space which contains a particular material separated by a boundary and can exchange heat with the surroundings. In Figure 1 the system is surrounded by a boundary which can contain any material which undergoes a thermodynamic process.

Internal energy of a thermodynamic system is the total energy of the molecules of the material of the system. In other words the internal energy is the energy associated solely with the molecules of the system (the total energy the molecules already have without any change in the sate of the system).
Generally in microscopic viewpoint we can say that the internal energy is the sum of kinetic and potential energy of all the molecules of the system. But there are also rotational and vibrational energies associated with the molecules which add to the internal energy. But in case of an ideal gas there is no potential energy of interaction between molecules (because there is no interaction between molecules) and we can define the internal energy of the ideal gas by only the total kinetic energy of all molecules.
And you know from kinetic theory of an ideal gas that the total kinetic energy of all molecules is directly proportional to the absolute temperature which tells us that the internal energy of an ideal gas depends only on the temperature of the system; increasing temperature increases the internal energy and decreasing temperature decreases the internal energy provided that the number of moles of the gas is constant.
What is the first law of thermodynamics?
The first law of thermodynamics reveals the fact that the heat energy can be transferred into mechanical energy. It says that the amount of heat added to a system is used in increasing the internal energy of the system and in doing work by the system. If \(U_1\) is the initial internal energy and \(U_2\) is the final internal energy after adding heat \(Q\) in the system, the change in internal energy is \(\Delta U = U_2 - U_1\). If \(W\) is the work done by the system after adding heat, we can mathematically express the first law of thermodynamics as
\[Q = \Delta U + W \tag{1} \label{1}\]
In other words a part of heat added is used in increasing the internal energy and a part of it is used in doing work by the system. If you rearrange the above expression of the first law of thermodynamics, you can find the expression of the change in internal energy of the system:
\[\Delta U = Q - W \label{2} \tag{2}\]
The new form of the first law of thermodynamics in the above equation shows that the change in internal energy of the system is the difference between the heat added to the system and the work done by the system. When heat enters a system, it is positive and when it leaves the system, it is negative. Similarly, if a work is done by the system, it is positive and if the work is done on the system by means of external source, it is negative.
What is work done by a thermodynamic system?
As the first law of thermodynamics suggested when you add heat to a system a part of it is used by the system in doing mechanical work. For example a quantity of heat \(Q\) is added to a cylinder with a piston containing gas as in Figure 2.
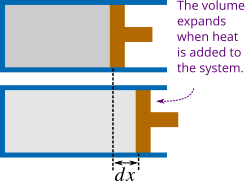
The gas expands and does work on its surroundings. Suppose the piston moves along positive x-direction due to expansion by a small distance \(dx\), and therefore the small increase in volume of the system is \(dV = Adx\). The force the gas exerts on the piston is \(pA\) where \(p\) is the pressure of the gas on the piston. So, the small work done by the system is \(dW = pAdx = pdV\). If the volume of the cylinder increases from initial volume \(V_1\) to final volume \(V_2\), the total work done by the system is
\[W = \int\limits_{{v_1}}^{{v_2}} {p{\kern 1pt} dV} \tag{3} \label{3}\]
If the pressure of the system is constant, you can take \(p\) out of the integral in the above equation:
\[W = p\int\limits_{{v_1}}^{{v_2}} {dV} = p({V_2} - {V_1}) \tag{4} \label{4}\]
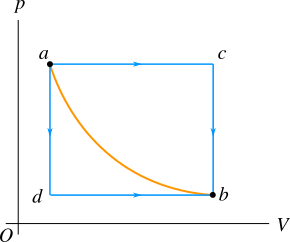
The work done by a thermodynamic system depends on the path chosen between two states. Figure 3 shows a \(pV\) curve of a system at a constant temperature. A \(pV\) curve at constant temperature is called an isotherm. There are infinitely many possible paths to go from state \(a\) to state \(b\). But to define the path dependence of work done by a thermodynamic system we choose two paths \(acb\) and \(adb\) to reach the same final state \(b\).
The work done by the system along line \(ac\) is the area under this line and no work is done along line \(cb\) (volume remains constant). Therefore, the total work done along the path \(acb\) is the area under the line \(ac\). In the similar way you can find the total work done along the path \(adb\) to be the area under the line \(db\); the work done along line \(ad\) is zero (volume remains constant) and along line \(db\) is the area under the line \(db\).
You can also directly go from state \(a\) to state \(b\) along the curve (see Figure 3) and in this case the work done by the system is the area under the curve. The area under the line \(ac\) is greater than the area under the curve \(ab\) and the area under the curve \(ab\) is greater than the area under line the \(db\). Therefore, the work done depends on the path chosen between two states; in short words, the work done by a thermodynamic system is path dependent.






