The engine statement of the second law of thermodynamics tells us that no heat engine can give \(100\%\) efficiency. But we have the Carnot engine which gives the maximum efficiency possible for any two given temperatures \(T_h\) and \(T_c\) in agreement with the second law of thermodynamics. Here we discuss a very useful ideal engine called Carnot engine and talk about the processes involved in its cycle called Carnot cycle. Carnot engine has the maximum efficiency possible for any two given temperatures consistent with the second law of thermodynamics.
To understand the operation involved in the Carnot engine we talk about the processes involved in the Carnot cycle. Carnot cycle is based on reversibility or it is a reversible cycle. It means it does not have any irreversible processes in the cycle. The reversibility of Carnot cycle makes it the maximum efficiency cycle. And reversibility is an idealization and therefore it is also an ideal cycle. A Carnot cycle involves two processes which are isothermal reversible process and adiabatic reversible process. Both isothermal and adiabatic processes in Carnot cycle are reversible, so the Carnot cycle is reversible.
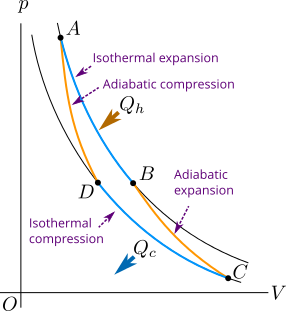
The Figure 2 shows a Carnot cycle having reversible isothermal and adiabatic processes. Consider that the system of Carnot cycle contains ideal gas. We will find the efficiency of the Carnot cycle in agreement with the second law of thermodynamics. In Figure 2 the process that takes place form state \(A\) to state \(B\) is isothermal expansion and that takes place from \(C\) to \(D\) is isothermal compression. Similarly the process that takes place from state \(B\) to state \(C\) is adiabatic expansion and that takes place from state \(D\) back to state \(A\) is adiabatic compression.
In isothermal expansion the system takes heat \(Q_h\) from hot reservoir initially at temperature \(T_h\). In adiabatic expansion the system does work spending its internal energy and the temperature of the system decreases. In isothermal compression, work is done on the system and temperature \(Q_c\) is rejected or thrown in the cold reservoir initially at temperature \(T_c\). Finally in adiabatic compression the work is done on the system and temperature of the system increases back to \(T_h\).
In isothermal expansion from state \(A\) to \(B\), the volume of the system increases from \(V_A\) to \(V_B\) and work done \(W_{AB}\) in isothermal expansion is
\[W_{AB} = \int_{{V_A}}^{{V_B}} {pdV} = \int_{{V_A}}^{{V_B}} {\frac{{nRT_h}}{V}dV} = nRT_h \ln \frac{{{V_B}}}{{{V_A}}} \tag{3} \label{3}\]
In above integration we replaced \(p\) by the expression of \(p\) from ideal gas equation. In isothermal expansion of an ideal gas the change in internal energy is zero, that is, \(\Delta U = 0\), therefore according to the first law of thermodynamics we have \(Q_h = W_{AB}\), so
\[{Q_h} = {W_{AB}} = nRT_h\ln \frac{{{V_B}}}{{{V_A}}} \tag{4} \label{4}\]
Similarly if \(V_C\) and \(V_D\) are the volumes at state \(C\) and \(D\) respectively, the work done on the isothermal compression is
\[{Q_c} = {W_{CD}} = nRT_c\ln \frac{{{V_D}}}{{{V_C}}} = -nRT_c\ln \frac{{{V_C}}}{{{V_D}}} \tag{5} \label{5}\]
As \(V_D\) is less than \(V_C\) in isothermal compression \(Q_c\) is negative. Dividing Equation \eqref{5} by Equation \eqref{4}:
\[\frac{{{Q_c}}}{{{Q_h}}} = -\frac{{{T_c}}}{{{T_h}}}\frac{{\ln \frac{{{V_C}}}{{{V_D}}}}}{{\ln \frac{{{V_B}}}{{{V_A}}}}} \tag{6} \label{6}\]
In adiabatic process from state \(B\) to \(C\) and from \(D\) to \(A\), we know from adiabatic process for ideal gas that, \({T_B}V_B^{\gamma - 1} = {T_C}V_C^{\gamma - 1}\) and \({T_D}V_D^{\gamma - 1} = {T_A}V_A^{\gamma - 1}\). Note that \(T_A\), \(T_B\), \(T_C\) and \(T_D\) are the temperatures of the corresponding states represented by the subscripts. But \(T_A = T_h\), \(T_B = T_h\), \(T_C = T_c\) and \(T_D = T_c\) and so,
\[{T_h}V_B^{\gamma - 1} = {T_c}V_C^{\gamma - 1} \tag{7} \label{7}\]
\[{T_h}V_A^{\gamma - 1} = {T_c}V_D^{\gamma - 1} \tag{8} \label{8}\]
Now dividing Equation \eqref{7} by Equation \eqref{8}, you'll get
\[\begin{align*} {\left( {\frac{{{V_B}}}{{{V_A}}}} \right)^{\gamma - 1}} &= {\left( {\frac{{{V_{C}}}}{{{V_D}}}} \right)^{\gamma - 1}}\\ {\rm{or,}}\quad \frac{{{V_B}}}{{{V_A}}} &= \frac{{{V_C}}}{{{V_D}}} \tag{9} \label{9} \end{align*}\]
Using Equation \eqref{9}, Equation \eqref{6} becomes
\[\frac{{{Q_c}}}{{{Q_h}}} = - \frac{{{T_c}}}{{{T_h}}} \tag{10} \label{10}\]
You know \(e = 1 + Q_c/Q_h\) from the second law of thermodynamics. You can find the efficiency of the Carnot engine using Equation \eqref{10}, that is the efficiency \(e\) is
\[e = 1 - \frac{{{T_c}}}{{{T_h}}} \tag{11} \label{11}\]
The above equation of the efficiency of the Carnot engine depends only on the temperatures of hot and cold reservoirs. The efficiency will be \(1\) if \(T_c = 0\rm{K}\) but practically this is impossible. The efficiency of the Carnot engine can be increased by making the ratio \(T_c/T_h\) smaller which can be achieved by increasing \(T_h\) and decreasing \(T_c\). As already noted a Carnot engine is reversible, therefore it is the most efficient engine than any other real engines operating between the same two temperatures.
To prove that a Carnot engine is the most efficient engine than any other real engine operating between the same two temperatures, first you should know what a refrigerator is.
Now we continue to prove that a Carnot engine is the most efficient engine than any other real heat engine operating between the same two temperatures. To prove this consider that a real engine has efficiency \(e\) greater than the efficiency of a Carnot engine \(e_c\), that is \(e > e_c\). We temporarily call the heat engine having greater efficiency than the efficiency of the Carnot engine as super engine. The Carnot engine takes heat \(Q_h\) from the hot reservoir, does work \(W\) and rejects heat \(Q_c\) to the cold reservoir.
The expression \(e = 1 + Q_c/Q_h\) from the second law of thermodynamics suggests that the super engine takes greater amount of heat than the Carnot engine for the same heat \(Q_c\) rejected by both engines. Therefore, for example, the super engine takes heat \(Q_h + Q'\) from the hot reservoir and rejects heat \(Q_c\) to the cold reservoir and does greater amount of work \(W + W'\). If \(W\) is the work done by the super engine taking heat \(Q_h\), then \(W + W'\) is the work done by the engine taking heat \(Q_h + Q'\). You know that a Carnot refrigerator is reversible and therefore it can be reversed which does the opposite of what a Carnot engine does, that is, takes heat \(Q_c\) from the cold reservoir and throws heat \(Q_h\) to the hot reservoir but you need do work \(W\) from external source to run a Carnot refrigerator.
The interesting thing is that if you couple the super engine and the Carnot refrigerator together to form a single machine, the net output of the coupled engine has \(100\%\) efficiency (\(Q_c = 0\)). It means that there is no loss of energy and you don't need to add energy to run this machine; it always runs after it's started. In other words the work \(W\) done by the super engine is used to run Carnot refrigerator and so the extra heat \(Q'\) the super engine takes is converted completely into mechanical work \(W'\). The output of the coupled engine violets the second law of thermodynamics and therefore no real engine can have efficiency greater than a Carnot engine operating between the same two temperatures.






