Let's consider two oppositely charged conducting plates parallel to each other and we are going to find the electric field between those plates as shown in Figure 1. Note that both plates have the same surface charge density \(\sigma\), that is charge per unit area. There is electrostatic attraction between the charge on opposite faces of the plates and the electric field has a direction from positive face towards negative face, so the electric field is zero on the left side of the negatively charged plate and on the right side of the positively charged plate.
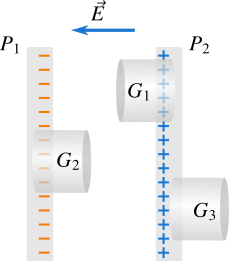
Note that the charges are accumulated on the opposite faces of the plates , that is the charges are accumulated at one face of each plate. Now take a look at the Gaussian surface \(G_1\) which is a cylinder where the electric field is parallel to the curved surface and perpendicular to its left end. There is no electric field to the right end of \(G_1\) because the electric field due to positively charged plate \(P_2\) is equal and opposite to the electric field due to negatively charged plate \(P_1\). Note that for an infinite plane sheet of charge the electric field is independent of the distance from the sheet. Therefore, the electric flux through the right end and the curved surface of \(G_1\) is zero. If \(A\) is the area of one of the ends, the total electric flux through the Gaussian surface \(G_1\) which encloses the charge \(\sigma A\) is
\[\begin{align*} 0 + 0 + EA = \frac{{\sigma A}}{{{\epsilon_0}}}\\ \therefore E = \frac{\sigma }{{{\epsilon_0}}} \tag{1} \end{align*}\]
You can also obtain the same result by making a Gaussian surface \({{G}_{2}}\) on the negatively charged plate. You can also make a Gaussian surface \(G_3\) as shown in Figure 1 to make sure that the electric field is zero on the right side of the positively charged plate. The Gaussian surface \(G_3\) does not enclose any charge because the charges are accumulated on the opposite faces of the plates due to electrostatic interaction, so the electric field on the right side of the positively charged plate is zero. The electric field is also zero on the left side of the negatively charged plate due to the same reason as that with the positively charged plate.






