In capacitors in series the capacitors are connected one after the other in series as shown in Figure 1. A potential difference is applied in the combination with a battery in which the positive terminal is connected to the left plate of left capacitor and negative terminal is connected to the right plate of right capacitor. The right plate of left capacitor and the left plate of right capacitor are directly connected to each other. These plates connected to each other form an isolated system (connected to nothing else but with each other) and they must have zero net charge.
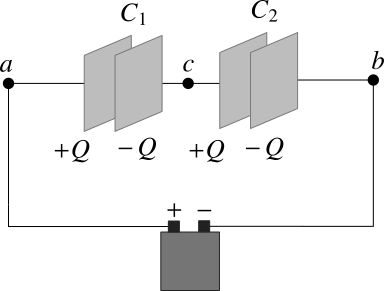
The left plate of left capacitor gets positive charge due to the applied potential difference and draws equal amount of negative charge from the right plate until all the electric field lines end up in the right plate. The right plate gets these electrons from the left plate of right capacitor leaving equal amount of positive charge. The left plate of right capacitor needs equal amount of negative charge on the right plate which is drawn from the negative terminal of the battery. Thus in series combination all the capacitors have the same charge(remember it is a common practice to represent the magnitude of charge on either conductors as the charge on a capacitor otherwise you know).
All the capacitors in series combination have the same charge but the potential differences of individual capacitors are not the same unless they have the same capacitance.
In Figure 1 \(C_1\) is the capacitance of the left capacitor and \(C_2\) is the capacitance of right capacitor.
The potential difference \(V_{ac}\) across the left capacitor with capacitance \(C_1\) is \(V_{ac} = Q/C_1\) and the potential difference \(V_{cb}\) across the right capacitor with capacitance \(C_2\) is \(V_{cb} = Q/C_2\). The total potential difference \(V\) applied to the combination is the sum of the potential differences across individual capacitors and hence
\[V = V_{ac} + V_{cb} = Q\left( {\frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}} \right)\]
The equivalent capacitance of the combination is \(C_{eq} = Q/V\) and from the above expression we can write,
\[\frac{1}{{{C_{{\rm{eq}}}}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}\]
Similarly for any number of capacitors combined in series combination we can get,
\[\frac{1}{{{C_{{\rm{eq}}}}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}}...\]
The above equation shows that the reciprocal of the equivalent capacitance is the algebraic sum of the reciprocals of the individual capacitances in the series combination and the equivalent capacitance is always less than any individual capacitance in the combination.






