The Doppler effect reveals the truth about the frequency of a wave received by a receiver when the source of the wave is in relative motion with the receiver.
The relative motion means that both the source and the receiver can be in motion or one can be at rest and the other can be in motion.
Consider that a wave receiver and a wave source are in relative motion. We have taken the positive x-direction to be the direction from the receiver to the source - it is important to do, why?
We divide the relative motion between the receiver and the source into three cases. In the first case we consider that only the receiver is moving; the source is stationary.
In the second case the source is moving but the receiver is stationary and in the third case both the receiver and the source are moving as discussed below.
Only the receiver in motion; the source is stationary
In this case as shown in Figure 2, consider that the receiver is moving towards the wave source in positive x-direction with velocity \(v_r\). The wave source is stationary and produces a wave which travels with speed \(v\) towards the receiver. Therefore, the relative speed of the wave with respect to the receiver is \(v + v_r\).

The wavelength \(\lambda \) of the wave is \(v/f_s\) where \(f_s\) is the frequency of the wave produced by the wave source. But the frequency noticed by the receiver is not the same as the frequency produced by the wave source due to the relative motion; we call this effect as Doppler effect. The frequency for the receiver \(f_r\) is
\[{f_r} = \frac{{v + {v_r}}}{\lambda } = \frac{{v + {v_r}}}{v}{f_s} \tag{3} \label{3}\]
Note that wave speed is always positive quantity but velocity can be either positive or negative. So if the receiver moves away from the source in negative x-direction, the velocity \(v_r\) is negative.
Only the source in motion; the receiver is stationary
In this case, first consider that the source is moving away from the receiver in positive x-direction with velocity \(v_s\). As the source moves, the wavelength in front of the source and the wavelength behind the source along the axis of the motion (positive x-axis) is not the same but still the wave speed is unaffected. The wavelength in front of the source is less than the wavelength behind the source as shown in Figure 3.
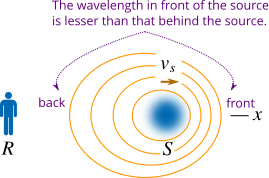
This happens because in time period \(T\) the wave travels a distance \(vT = v/f_s\) and the source also travels a distance \(v_s T = v_s/f_s\) and therefore the wavelength behind the source is stretched out but the wavelength in front of the source is compressed. So the wavelength behind the source as the source is moving away from the receiver in positive x-direction is
\[\lambda = \frac{v}{{{f_s}}} + \frac{{{v_s}}}{{{f_s}}} = \frac{{v + {v_s}}}{{{f_s}}} \tag{4} \label{4}\]
Now, the wave speed \(v\) is unaffected by the motion of the source and since the receiver is stationary, the relative speed of the wave with respect to the receiver is also \(v\), and the frequency for the receiver is the wave speed \(v\) divided by the wavelength in above equation.
\[{f_r} = \frac{v}{{v + {v_s}}}{f_s} \tag{5} \label{5}\]
As the wave source moves towards the stationary receiver in negative x-direction instead of moving away, \(v_s\) is negative and the above equation still holds.
Both the receiver and the source in motion
In Figure 4 both the receiver and the source are moving towards positive x-direction. The speed of sound wave for the receiver relative to the source is not affected by the motion of the source but it's affected by the motion of the receiver. And therefore for the situation as in Figure 4 the relative wave speed for the receiver is \(v+v_r\).

Since the source is moving towards +x-direction, the wavelength at the back of the source is stretched which is \(vT + v_sT = v/f_s + v_s/f_s = (v+v_s)/f_s\). Therefore, the frequency \(f_r\) of the wave for the receiver is the relative wave speed for the receiver divided by the wavelength \((v+v_s)/f_s\), so
\[{f_r} = \frac{{v + {v_r}}}{{v + {v_s}}}{f_s} \tag{6} \label{6}\]
If the source and the receiver are moving in negative x-direction both the velocities \(v_s\) and \(v_r\) will be negative. You should take the direction from receiver to the source as positive direction. Note again that the wave speed \(v\) is always positive but the velocity can be positive or negative. The above equation \eqref{6} is valid for all the situations of relative motion between the source and the receiver.






