The addition of vectors is not like the addition of scalars. For scalars you simply add or subtract numbers but a vector quantity is also associated with a direction, so adding or subtracting them is different from the normal addition or subtraction of numbers.
You can easily understand the addition or subtraction of vectors by their graphical representation which is described below. In vector addition you always need to consider both the magnitude and the direction of vectors.
Consider two vectors \(\vec{A}\) and \(\vec{B}\) in Figure 1 which we add together to get the resultant vector. Note that the vector \(\vec{B}\) shown in dotted line in Figure 2 whose tail is at the head of \(\vec{A}\) is equal to the original \(\vec{B}\) and now the sum of \(\vec{A}\) and \(\vec{B}\) is the resultant vector whose tail is at the starting point, that is at the tail of \(\vec{A}\) and head is at the ending point, that is at the head of \(\vec{B}\).
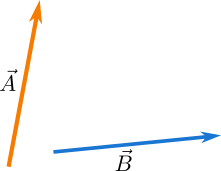
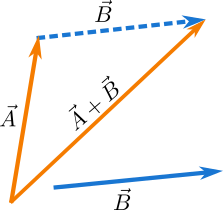
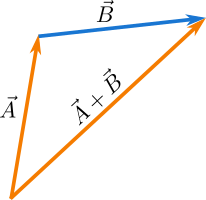
In Figure 3 you can see that the sum of \(\vec{A}\) and \(\vec{B}\) is the resultant vector straight from the tail of \(\vec{A}\) to the head of\(\vec{B}\). In other words when you move along the direction of \(\vec{A}\) through the magnitude \(A\) and then along the direction of \(\vec{B}\) through the magnitude \(B\), your resultant magnitude and direction of your movement will be that shown by the resultant vector \(\vec{R}=\vec{A}+\vec{B}\).
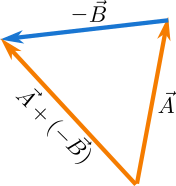
Now vector subtraction is the same as vector addition. If you subtract \(\vec{A}\) and \(\vec{B}\), like \(\vec{A}-\vec{B}\), this is the same as \(\vec{R}=\vec{A}+(-\vec{B})\). Now you know that the negative of a vector has the same magnitude but has opposite direction. So \(-\vec{B}\) has the same magnitude as that of \(\vec{B}\) but has opposite direction and the resultant of the vectors will be that as shown in Figure 4.
Components of a Vector
A vector can be resolved into its components. We find the x and y-components of a vector \(\vec{A}\) in Figure 5. The x-component of the vector is the component along x-axis and y-component along y-axis.
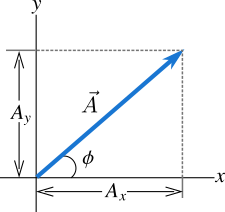
Notice in Figure 5 that \(\vec{A}\) makes an angle \(\phi\) with x-axis. Now we can easily find the value of \({{A}_{x}}\) and\({{A}_{y}}\) to be, \({{A}_{x}}=A\cos \phi \) and \({{A}_{y}}=A\sin \phi \). So the x and y-components of \(\vec{A}\) can be written in vector form as,
\[{{\vec{A}}_{x}}=(A\cos \phi )\hat{i}\]
\[{{\vec{A}}_{y}}=(A\sin \phi )\hat{j}\]
Note that the unit vectors \(\hat{i}\) and \(\hat{j}\) give the direction along positive x-axis and positive y-axis respectively. \(\vec{A}\) can be written as \(\vec{A}={{A}_{x}}\hat{i}+{{A}_{y}}\hat{j}=(A\cos \phi )\hat{i}+(A\sin \phi )\hat{j}\). Here we also can find the magnitude and direction of \(\vec{A}\) as,
\[A=\sqrt{{{A}_{x}}^{2}+{{A}_{y}}^{2}} \tag{1} \label{1}\]
\[\phi =\arctan \left( \frac{{{A}_{y}}}{{{A}_{x}}} \right) \tag{2} \label{2}\]
Here the angle \(\phi\) gives the direction for \(\vec{A}\) and you obviously know \(\tan \phi =\frac{{{A}_{y}}}{{{A}_{x}}}\).
How to add using components?
Addition of vectors using components is the easiest way to add vectors. In Figure 6 there are two vectors. The tail of \(\vec{B}\) is at the head of \(\vec{A}\). First we find the x and y-components of \(\vec{A}\) and \(\vec{B}\), then we add all x-components to find the total x-component of the resultant vector and all y-components to find the total y-component of the resultant vector.
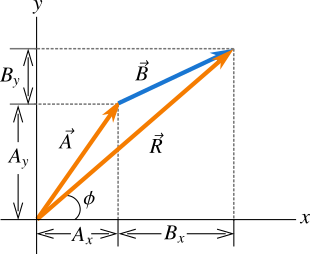
Now the total x and y-components of the resultant vector \(\vec{R}\) are \({{R}_{x}}={{A}_{x}}+{{B}_{x}}\) and \({{R}_{y}}={{A}_{y}}+{{B}_{y}}\). Now we can find the magnitude and direction of the resultant vector easily. Suppose \(\vec{R}\) makes an angle \(\phi\) with x-axis.
\[R=\sqrt{{{R}_{x}}^{2}+{{R}_{y}}^{2}}\]
\[\phi =\arctan \frac{{{R}_{y}}}{{{R}_{x}}}\]
Now \(\vec{R}\) is \(\vec{R}={{R}_{x}}\hat{i}+{{R}_{y}}\hat{j}\). Obviously the unit vectors make it easy to represent a vector as well as its components.
How to add using parallelogram?
In parallelogram addition of vectors we arrange vectors in the form of parallelogram by making opposite vectors equal. In Figure 7. the vectors \(\vec{A}\) and \(\vec{B}\) shown in dotted line are equal to the original vectors (these vectors are acting as the opposite sides of the parallelogram) and help to form a parallelogram. You obviously know that the resultant vector \(\vec{R}\) is the sum of \(\vec{A}\) and \(\vec{B}\) and here we find the magnitude and direction of the resultant vector.
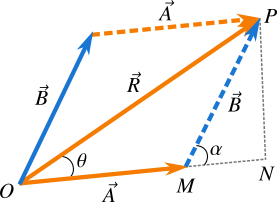
In Figure 7. produce the line \(\text{OM}\) up to \(\text{N}\) and draw \(\text{PN}\bot \text{ON}\). Let the angle \(\angle \text{PMN=}\alpha \) and the angle made by the resultant vector \(\vec{R}\) with \(\vec{A}\) be \(\theta\). Now \(\sin \alpha = \text{PN}/B\) which gives \(\text{PN}=B\sin \alpha \) and \(\cos \alpha =\text{MN}/B\) which gives \(\text{MN=}B\cos \alpha \), so \(\text{ON}=\text{OM}+\text{MN}=A+B\cos \alpha \). Since \(\vartriangle \text{OPN}\) is a right-angled triangle, the magnitude of \(\vec{R}\) is,
\[\begin{align*} R&=\sqrt{\text{O}{{\text{N}}^{2}}+\text{P}{{\text{N}}^{2}}} \\ & =\sqrt{{{(A+B\cos\alpha )}^{2}}+(B\sin\alpha )} \\ & =\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \alpha } \tag{3} \label{3} \end{align*}\]
When \(\alpha ={{90}^{\circ }}\), it means when the vectors are perpendicular Eq. \eqref{3} becomes \(R=\sqrt{{{A}^{2}}+{{B}^{2}}}\) as it should be. Again, \(\tan \theta =\text{PN}/\text{ON}\), so,
\[\begin{align*} \tan \theta&=\frac{B\sin \alpha }{A+B\cos \alpha } \\ \text{and,}\quad \quad \theta& =\arctan \left( \frac{B\sin \alpha }{A+B\cos \alpha } \right) \tag{4} \label{4} \end{align*}\]
You may have known that the angle \(\theta\) indicates the direction of the resultant vector. When \(\alpha ={{0}^{\circ }}\), \(\theta ={{0}^{\circ }}\) which is we should get.






