Wave beats occur when two waves having the same amplitude but slightly different frequencies overlap in a region of space. Here we discuss sound wave beats.
In Figure 1 you can see two sinusoidal sound waves having the same amplitude but slightly different frequencies overlap in a rigion of space.
Note that the difference between two frequencies should not exceed \(6\) or \(7 \text{Hz}\). The two sound waves superpose and the displacement of any particle at a point in the medium is given by the vector sum of the individual displacements due to each wave.
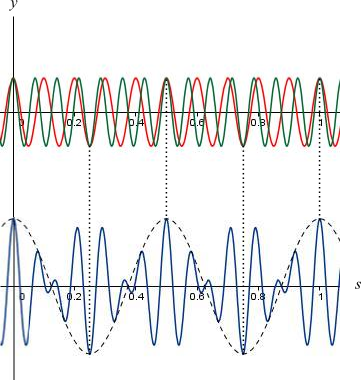
Both are sinusoidal waves so the first wave shown by red line is say \(y_1 = A \cos (\omega _1t)\) and the other shown by green line is say \(y_2 = A\cos (\omega _2t)\).
Note that both waves are travelling in positive x-direction in our illustration in Figure 1.
Now we are going to add these two waves to get the resultant wave, that is \(y = y_1 + y_2\). But before adding the two wave functions, you should know the trigonometric identity \(\cos a + \cos b = 2\cos [\frac{1}{2}(a - b)]\cos [\frac{1}{2}(a + b)]\) and you'll get the result:
\[y = 2A\cos [\frac{1}{2}({\omega _1} - {\omega _2})t]\cos [\frac{1}{2}({\omega _1} + {\omega _2})t] \tag{1} \label{1}\]
You know that \(\omega _1 = 2 \pi f_1\) and \(\omega _2 = 2 \pi f_2\) where \(f_1\) and \(f_2\) are the corresponding frequencies. Substituting the values of \(\omega _1\) and \(\omega _2\) in the above equation you'll get another form:
\[y = 2A\cos [\frac{1}{2}2\pi ({f_1} - {f_2})t]\cos [\frac{1}{2}2\pi ({f_1} + {f_2})t] \tag{2} \label{2}\]
Notice the first part of the right hand side of the above equation which is \(2A\cos [\frac{1}{2}2\pi ({f_1} - {f_2})t]\).
In one complete cycle of \(2A\cos [\frac{1}{2}2\pi ({f_1} - {f_2})t]\) there are two amplitude peaks hence the beat frequency is twice the part \(\frac{1}{2} (f_1 - f_2)\) which is simply \(f_1 - f_2\).
The slight difference in frequencies between two waves having the same amplitude causes the variation in loudness called beats.
The Figure 1 shows the displacement-time graph of the superposition of two sinusoidal waves.
You can easily find the beat frequency of the resultant wave by just looking at the graph which is simply \(4 \rm Hz\) in which the amplitude goes through four maxima and four minima in one second.
The actual wave function of the wave shown by red curve is \(y_1 = 5 \cos (2\pi 10 x)\) and the actual wave function of the wave shown by green curve is \(y_2 = 5 \cos (2\pi 14 x)\), so \(f_1 = 10 \rm Hz\) and \(f_2 = 14 \rm Hz\).
Therefore, the beat frequency is the difference between these two frequencies which is \(\left| {{f_1} - {f_2}} \right| = 4 \rm Hz\).






